Orthogonal Frequency Division Multiplexing (OFDM)

Abstract

Carrier frequency offset abbreviated as CFO in the concept of OFDM systems will then decrease the concept of orthogonal in various kinds of sub carriers. Here loss of Orthogonality will be results in particular performance degradation. This is very much crucial to estimate the performance. A sub optimal approach is introduced in order to expect the CFO by using the sub carriers which are made null.

The CFO estimation will need the integer CFO estimation implementation. The carrier frequency offset will estimate the no of sub carriers. When the past work will be compared with the sub carriers’ expectation, the complexity can be maintained and introduced to the particular OFDM symbols. The introduced approach complexity will be specifically lower due to the lack of simple correlation.

This is the main and important component of the OFDM systems. Only single OFDM symbol and the allocation sub carrier are used for estimating the extent of respective approach. This estimation could be done in the inverse sampling duration. There are some other traditional approaches with similar estimation range. This estimation would also contain higher complexity of the OFDM symbols.

Best efficiency can be easily achieved with the sub carrier allocation. This allocation is specifically relying on the binary sequences. These binary sequences are typically introduces the concepts related to extended m-sequences. These sequences are typically represented by simulations that are employed by the criteria regarding sub carrier sequences. These simulations are deployed for achieving higher likelihood estimators.

Introduction

OFDM is considered as the standard technology for the wireless communications. These communications are considered by the multi path effects. These effects are specifically considered by the adoptions of advanced technology standards. Particularly this OFDM is sensitive in order to synchronize the CFO errors.

In particular, this estimation is stimulated through the series of oscillators among the receiver as well as sender in relevant transfers that are made. This particular OFDM is in the active on the research location. Various training signal are known to be training signals and medium statistics of the CFO estimator.

This is typically operated and performed by the likelihood estimator. This is specifically considered as the expansion of the training signals. Here only specific methods are essential o understand. The least square can be deployed for the estimation.  The specific criteria can be used for achieving the correlation techniques. Training signals are specifically periodic and these estimations would be relying on the ML criteria. This approach can be achieved by the training configuration.

Several training symbols are not that much needed for performing the simple correlation. These symbols will be used for sending the information regarding the configuration. This could be expected by the two different identical components. This approach can be used for presenting the estimation range of identical components. There are two different kinds of sub carrier spacing. Narrow spacing estimation approach can be oscillates with the maximum precision. Here higher precision could be used efficiently.

The carrier frequency offset could be estimated by the OFDM inheritance. This is usually referred to the blind approaches of the OFDM systems. Carrier frequency offset estimation is done with the impulsive response of the carrier signals. Edge of the Sub carriers will result in high performance. The efficiency is generally not used to refer the virtual carriers. The carrier impulsive ranges are typically specified by the sub space methods.

Continuous sub carriers are adjacent to the interference suppression’s. This can be easily achieved by using the medium interference. It considers the sub space functions in case of inverse sampling duration. Frequency selective medium can be used for lacking the identifiably feature. These features are used to propose the distinct space coding for the OFDM systems. Here only single training symbol is used to CFO estimation with the help of null sub carriers. All the carriers are made null to the estimation of carrier frequency offset.

This OFDM symbol contains two different similar components. One will be the fractional part which is then cause the Orthogonality loss. This can be estimated for performing the simple correlation operation on the OFDM symbols.

This will typically shifts the indexes regarding sub carriers. These can be complexly estimated by using the null sub carriers. Assigning of indexes could be done at the even positions of t eh sub carriers. Perfect correlation sequences are clearly performed and proposed by the perfect auto-correlation sequences and m- sequences known as modified sequences can be utilized in order to attain maximum efficiency of OFDM system, and an estimation range can be the inverse sampling duration’s according to the Fourier transformations.

This will also use the CFO compensation components. These to identical components are typically used to represent the low complexity. Fractional and integer parts of CFO can be depended on the perfect modified sequences as well as autocorrelation sequences in order to achieve the results of simulation.

In this case, if  only an individual training symbol is used, then the performance of transmission will be achieved by the estimations of CFO. Final CFO Estimation is also specifically described in this section. Optimal estimation with the null carriers from the OFDM symbols.

But the final CFO estimation could be expected depend on the ML criteria. Several allocation approaches are used for investigation of the CFO estimations. This estimation is very much similar to the allocation null sub carriers. The carrier frequency offset can be estimated by using the following two considerations. Perfect autocorrelation approaches and modified sub carriers. These modified carriers are denoted by m-sequences.

Various simulation outcomes will be estimated and these will typically represent the higher efficiency of the introduced allocation approaches of the sub carriers. These allocations are successfully done with the null sub carriers with distinct space coding.

Matlab Source Code:


%%%%% imlementation of pilot carrier frequnecy offset estimation in OFDm systems
%*****************************************************
% wimax parameters %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% N=256,L=16,4-qam or 16 qam modulation length of cycli prefix is
%%% 8,16,32,64
warning off;
clc;clear all;close all;
N=256; %%% length of the subcarriers
Np=N/4; %% No.of Pilot carriers
L=16; %% length of the cp
Nsym=100; %% no of symbols
iter=10; %% no of iterations
M=16; %% for symbol generation and type of modulation
Ep=2; %% energy per symbol
Ip=[1:N/Np:N]; % location of pilots
%%%%%%%%%%%%%%%%%%%%%%%%
offset=0.2571;
SNR = [0:2:20]; % signal to noise ratio vector in dB
for it=1:iter;
for j=1:length(SNR)
snr=SNR(j);
TrDataBit = randint(Nsym,1,M); %% generate random 400 symols eqn(1)
TrDataMod = qammod(TrDataBit,M); %% do IQ modulation eqn(2)
TrDataMod = Ep * TrDataMod; %% multiply with energy per symbol
TrDataIfft = ifft(TrDataMod,N); %% do ifft operation eqn(3)
s=TrDataIfft(1:(N)); %% eqn(1)
m=TrDataIfft(1:N); %% eqn(2)
alp=(N-Np)/N;
tra=[s;m];
TrDataIfftGi = [tra(N- L + 1 : N);tra]; % insert cyclic prefix eqn(4)
%%%%%%%%%%%%%%%%%%%% End of Transmitter %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
RxDataIfftGi = awgn(TrDataIfftGi,SNR(j)); %% additive white gaussian noise is inserted
%%%%%%%%%%%%%%%%%%%%%%%% End of channel %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
RxDataIfft = RxDataIfftGi(L+1:N+L); % eqn(5)
RxDataMod = fft(RxDataIfft); % eqn(6)
RxDataBit=qamdemod(RxDataMod,M);

%%%%%% Hybrid Maximum Likelihood Estimation %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for k=1:Np
frk(k)=pdf(‘Normal’,RxDataBit(k),RxDataBit(N),1);
frx1(k)=pdf(‘Normal’,RxDataBit(k),0,1);
frx2(k)=pdf(‘Normal’,RxDataBit(N),0,1); %% eqn(5) in hybrid max likelihood
del(k)=log(frk(k)/(frx1(k)*frx2(k)));
end
for k=1:Np
frx3(k)=pdf(‘Normal’,RxDataBit(k),0,1);
del1(k)=log(frx3(k));
end
el(j)=max([del del1]); %% cyclic prefix based %eqn(6) in hybrid max likelihood
ro=(alp*SNR(j))/(alp*SNR(j)+1); %eqn(8) in hybrid max likelihood
%%%%% cyclic Prefix based Estimation %%%%%%%%
for k=1:Nsym
a1(k)=(RxDataBit(k)^2);
a2(k)=(RxDataBit(k)).*conj((RxDataBit(k))*exp(2*pi*offset));
decp(k)=real(a2(k)-(ro/2)*a1(k));
end
ep(j)=mean(decp/k)/j;

RxDataBit=RxDataBit(RxDataBit>0)*exp(2*pi*offset); %%eqn(17)
%%%%%%%%%%%%%%%%%%% Proposed Method %%%%%%%%%%%%%%%%
for k=1:Np
for i=1:Nsym
Z = RxDataBit(i).^2;
b1(i)=(RxDataBit(i)/Z);
end %% eqn(18)
br=sum(b1.^2);
b2=(sum(b1)/i)^2;
et(k)=(sum(1-(b2/br)))/Np*j;
end
e(it,j)=min(et);
end
end
cpp=fliplr(sort(abs(ep))); %%% cycli prefix
prp=fliplr(sort(mean(e)));
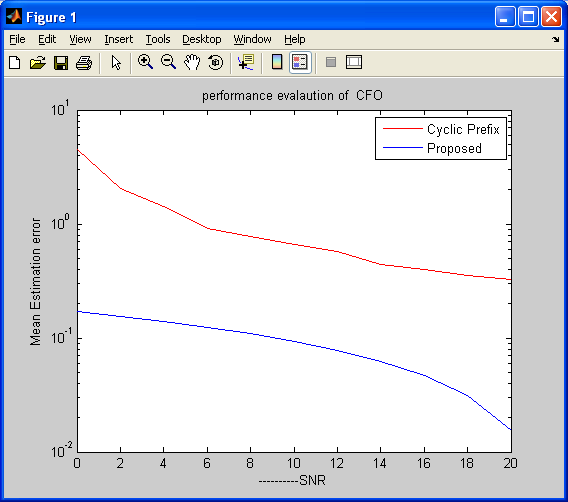
figure,
semilogy(SNR,cpp,’r’);hold on;
semilogy(SNR,prp,’b ‘);
xlabel(‘———-SNR’);ylabel(‘Mean Estimation error’);
title(‘performance evalaution of CFO’)
legend(‘Cyclic Prefix’,’Proposed’);

 

Problem definition:

OFDM systems are widely used across telecommunication world and frequency offset estimation is the tedious job across the OFDM systems. Frequency offset causes performance degradation and loss of orthogonality across the sub carriers. In this project I will estimate the frequency offset using pilot carriers and implement the compensation based on this estimation.

Aims & objectives

• Aims:

To estimate the frequency offset using pilot carriers across OFDM with MATLAB simulation.

• Objectives:

The following are the research objectives of the project:

• To recognize the concept of OFDM systems and the importance of frequency estimation across them.
• To prepare literature review on the existing Frequency offset estimation techniques and evaluate their limitation
• To design a Frequency offset estimator based on pilot carriers
• To implement compensation based on frequency offset estimation using pilot carriers.
• To simulate the proposed system in MATLAB and document the observations